迷路の最短手数のアルゴリズム

迷路の最短手数を見つける

---

　迷路の最短手数を見つけるときに有名なアルゴリズムである幅優先探索を使用します。知識としては知っていましたが、実装をする経験を積んでおきたいと思い今回は記事を出しました。 それでは早速やっていきましょう。

---

前提

　まずは、前提として迷路とは上下左右に移動できる二次元盤面上の迷路であるとします。さらに、その盤面には次のような情報を与えます。

• 盤面サイズ、スタートの座標、ゴールの座標
• 通行可能か不可能かを示す文字列の情報を持った盤面

---

直感的なイメージ

　迷路のスタート地点からゴール地点までの最短歩数を見つける時のイメージとして下の図をつける。

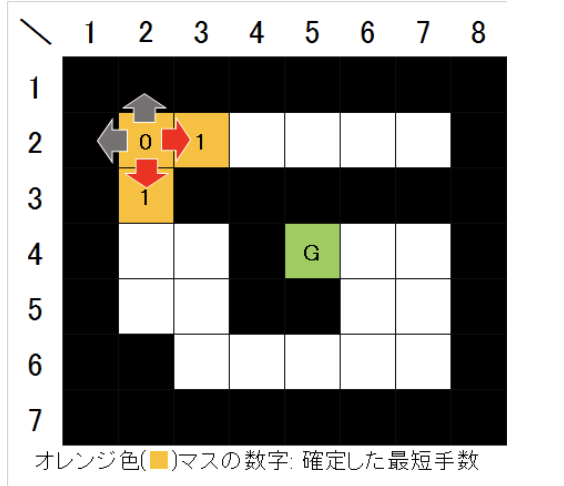
　スタートから近いマスから順番にたどり着く歩数を下の図のようにマーキングしていきゴール地点についたらその時の歩数を出力を行う。

---

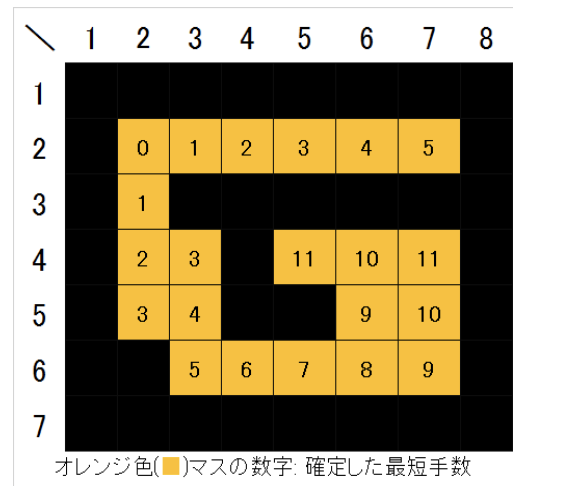
キューを用いる

　この迷路の最短探索をするときには、先ほども述べた幅優先探索を行う。

---

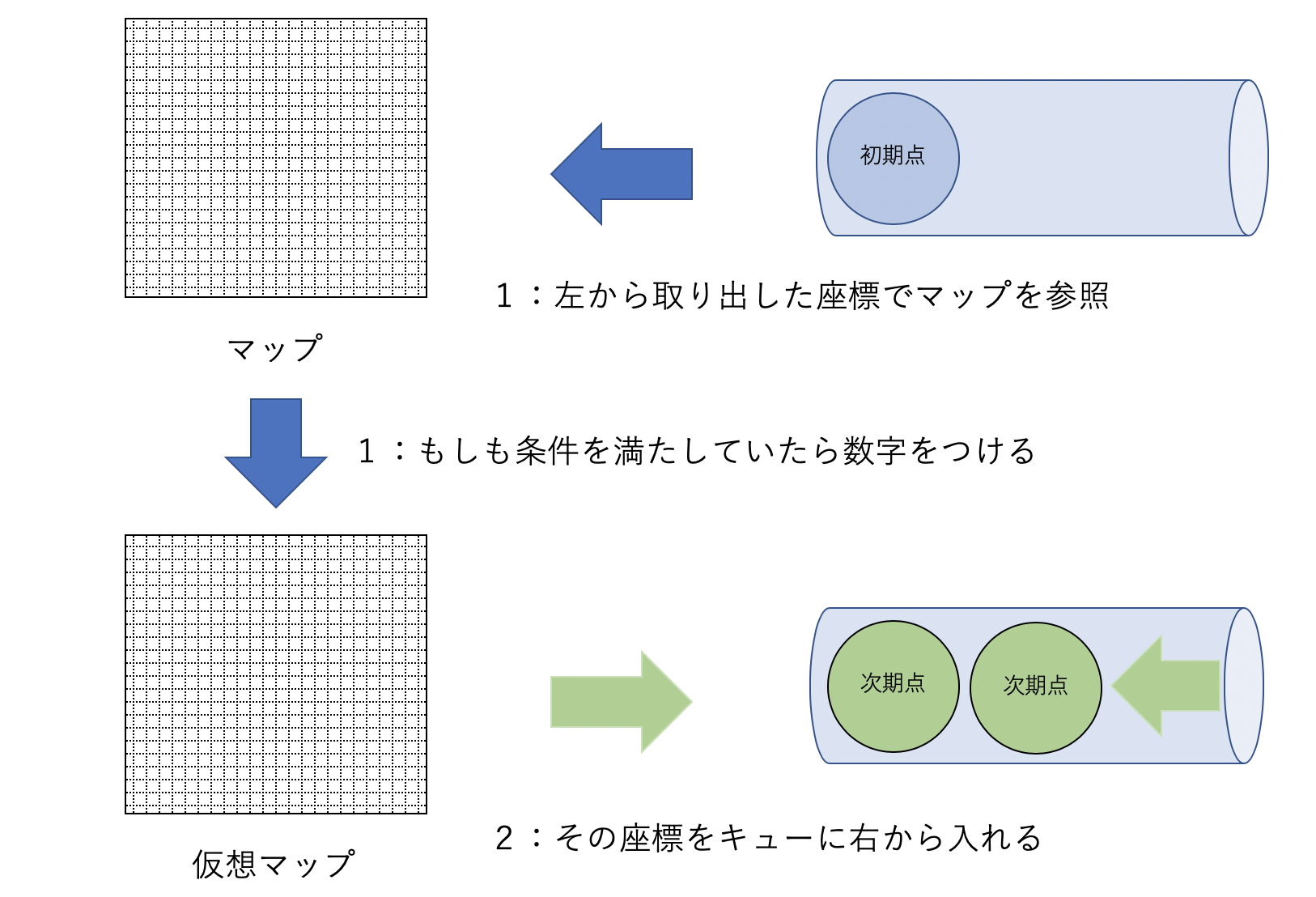
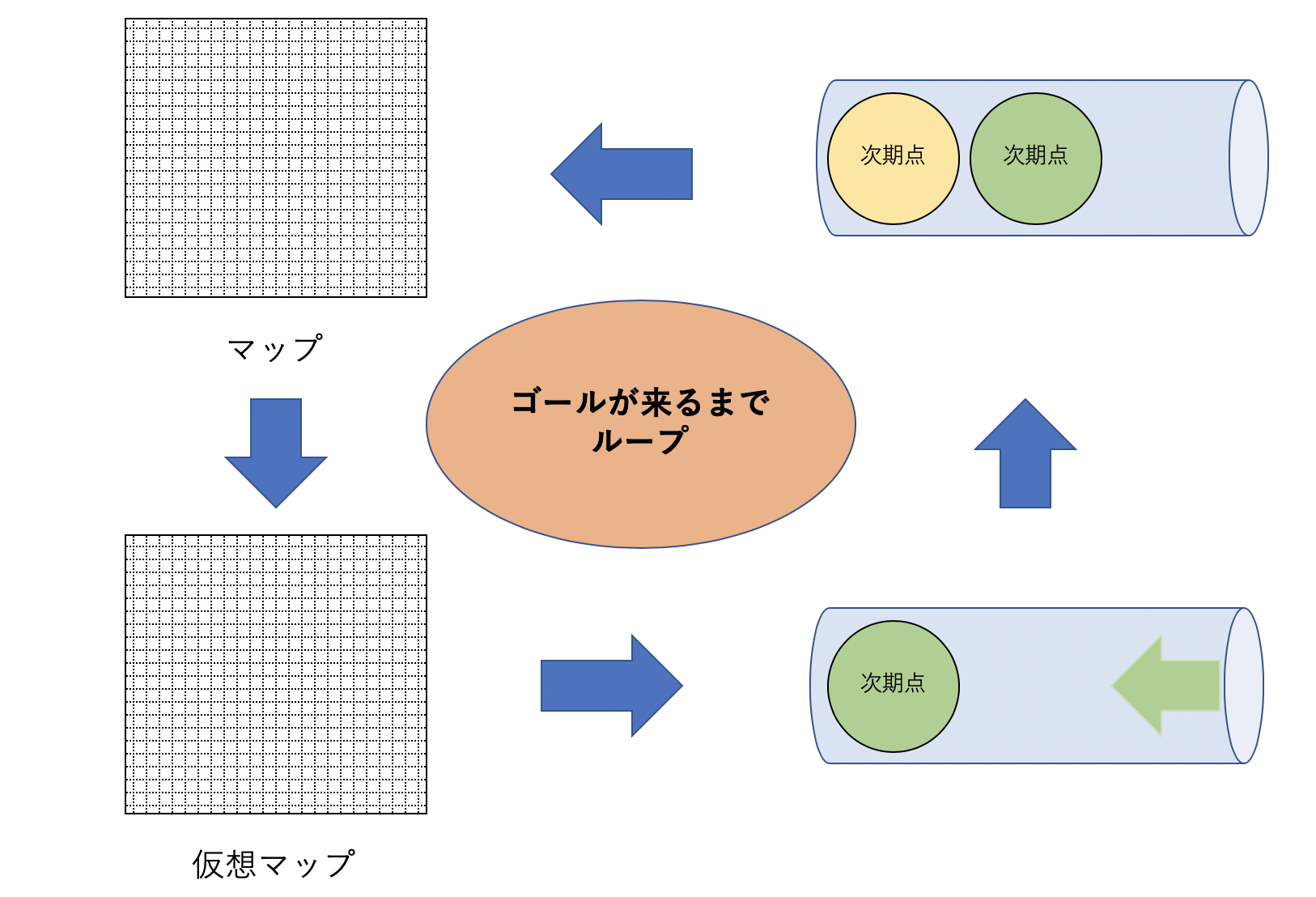
コード

from collections import deque 
#マップの高さと幅を記録する#
height, width = map(int,input().split())
#スタート地点を記録する#
sy , sx = map(int, input().split())
sy -=1
sx -=1
#ゴールを記録する#
gy , gx = map(int, input().split())
gy -=1
gx -=1
#マップを記録する#
MAP = [list(input()) for i in range(height)]


def bfs():
  #手順を示す
  step_map = [ [ float("inf") ]*width for i in range (height)]
  #x軸の移動
  dx = [1,-1,0,0]
  #y軸の移動
  dy = [0,0,-1,1]
  #キューを作成
  que = deque([(sy,sx)])
  step_map[sy][sx] = 0
  while que:
    step_spot = que.popleft()
    if step_spot[0]==gy and step_spot[1]==gx:
      break
    #四方向に確認
    for i in range(4):
      n = step_map[step_spot[0]][step_spot[1]] 
      ny = step_spot[0] + dx[i]
      nx = step_spot[1] + dy[i]
      #進んだ先が"."であること step_mapが数字じゃないとき 範囲内にある時
      if nx <= width-1 and nx>=0 and ny <=height-1 and ny>=0 :
        if MAP[ny][nx]=="." and step_map[ny][nx]==float("inf") :
          #進んだ先の回数をn+1
          step_map[ny][nx] = n + 1
          #キューに入れる
          que.append((ny,nx))
  return step_map[gy][gx]

print(bfs())

---

実行結果

---

感想

意味が理解できれば実装するのはかなり楽に行けた。